
Reidemeister moves
Apparent contours of embedded 2D manifolds can be used
to simulate knots in the following way:
Given a knot (one or more smooth closed curves in 3D that
do not intersect) we can construct the tubular surface
consisting of all points having given distance e
from the knot, where the positive number e is chosen
sufficiently small.
In this way we obtain one or more surfaces with the topology
of the torus that are knotted according to the original knot.
The projection of the resulting surface on a plane corresponds
to the projection of the knot, and the information on
which arc goes over the other on crossings of the knot
produces corresponding informations on the Huffman labelling
of the apparent contour of the tubular surface.
An important concept in knot theory are the
Reidemeister
moves: topological operations that can be performed on the
projected knot that correspond to isotopic deformations of the
originating knot.
Our rules are actually the equivalent of Reidemeister moves
in the context of embedded surfaces instead of knots.
Each of the three Reidemeister moves correspond to a particular
sequence of rules performed on the tubular surface associated
to the knot.
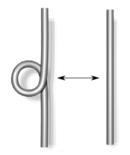 The first Reidemeister move (untwist) can be simulated
with the sequence of rules:
CR2,
CR0LB (CR0RB),
CR0L (CR0R),
S,
(the choice in parentheses depends on the original orientation of the
twist).
You can test this sequence on the torus_eight example with
the web interface.
The first Reidemeister move (untwist) can be simulated
with the sequence of rules:
CR2,
CR0LB (CR0RB),
CR0L (CR0R),
S,
(the choice in parentheses depends on the original orientation of the
twist).
You can test this sequence on the torus_eight example with
the web interface.
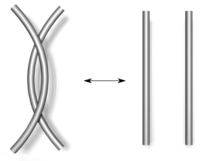 The sequence
K0,
K1,
K1B,
K2
corresponds to the second Reidemeister move (see e.g.
the two_rings example).
The sequence
K0,
K1,
K1B,
K2
corresponds to the second Reidemeister move (see e.g.
the two_rings example).
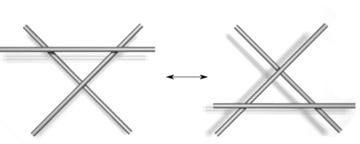 The third Reidemeister move can be achieved with
a sequence of eight T moves, since each of
the two lines corresponding to the string that
lies on top have to traverse four crossings of the
apparent contour corresponding to the other two
strings (a single crossing of a knot gives rise to
four crossings of the apparent contour of the tubular
surfaces).
The third Reidemeister move can be achieved with
a sequence of eight T moves, since each of
the two lines corresponding to the string that
lies on top have to traverse four crossings of the
apparent contour corresponding to the other two
strings (a single crossing of a knot gives rise to
four crossings of the apparent contour of the tubular
surfaces).
Pictures are courtesy of wikipedia.

 The first Reidemeister move (untwist) can be simulated
with the sequence of rules:
CR2,
CR0LB (CR0RB),
CR0L (CR0R),
S,
(the choice in parentheses depends on the original orientation of the
twist).
You can test this sequence on the torus_eight example with
the web interface.
The first Reidemeister move (untwist) can be simulated
with the sequence of rules:
CR2,
CR0LB (CR0RB),
CR0L (CR0R),
S,
(the choice in parentheses depends on the original orientation of the
twist).
You can test this sequence on the torus_eight example with
the web interface.
 The sequence
K0,
K1,
K1B,
K2
corresponds to the second Reidemeister move (see e.g.
the two_rings example).
The sequence
K0,
K1,
K1B,
K2
corresponds to the second Reidemeister move (see e.g.
the two_rings example).
 The third Reidemeister move can be achieved with
a sequence of eight T moves, since each of
the two lines corresponding to the string that
lies on top have to traverse four crossings of the
apparent contour corresponding to the other two
strings (a single crossing of a knot gives rise to
four crossings of the apparent contour of the tubular
surfaces).
The third Reidemeister move can be achieved with
a sequence of eight T moves, since each of
the two lines corresponding to the string that
lies on top have to traverse four crossings of the
apparent contour corresponding to the other two
strings (a single crossing of a knot gives rise to
four crossings of the apparent contour of the tubular
surfaces).